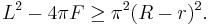Bonnesen's inequality

Bonnesen's inequality is an inequality relating the length, the area, the radius of the incircle and the radius of the circumcircle of a Jordan curve. It is a strengthening of the classical isoperimetric inequality.

More precisely, consider a planar simple closed curve of length $L$ bounding a domain of area $F$ . Let $r$ and $R$ denote the radii of the incircle and the circumcircle. Bonnesen proved the inequality

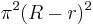$L^2-4\pi F\geq \pi^2 (R-r)^2. \,$

The term $\pi^2 (R-r)^2$ in the right hand side is known as the isoperimetric defect.

Loewner's torus inequality with isosystolic defect is a systolic analogue of Bonnesen's inequality.

References

Bonnesen, T.: "Sur une amélioration de l'inégalité isopérimetrique du cercle et la démonstration d'une inégalité de Minkowski," C. R. Acad. Sci. Paris 172 (1921), 1087–1089.
Yu. D. Burago and V. A. Zalgaller, Geometric inequalities. Translated from the Russian by A. B. Sosinskiĭ. Springer-Verlag, Berlin, 1988. ISBN 3-540-13615-0.